SQLですべての組み合わせを生成する

組み合わせを返す

数値テーブルまたは数値生成CTEを使用して、0〜2 ^ n-1を選択します。これらの数値に1を含むビット位置を使用して、組み合わせの相対メンバーの有無を示し、ないメンバーを削除します。正しい数の値があれば、必要なすべての組み合わせで結果セットを返すことができるはずです。

WITH Nums (Num) AS (
   SELECT Num
   FROM Numbers
   WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
   SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
   FROM @set
), Combos AS (
   SELECT
      ComboID = N.Num,
      S.Value,
      Cnt = Count(*) OVER (PARTITION BY N.Num)
   FROM
      Nums N
      INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
   ComboID,
   Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;

このクエリはかなりうまく機能しますが、気の利いたパラレルビットカウント 最初に一度に適切な数のアイテムを取得します。これにより、パフォーマンスが3〜3.5倍速くなります（CPUと時間の両方）：

WITH Nums AS (
   SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
   FROM dbo.Numbers
   WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
   SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
   FROM Nums
), Nums3 AS (
   SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
   FROM Nums2
), BaseSet AS (
   SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
   FROM @set
)
SELECT
   ComboID = N.Num,
   S.Value
FROM
   Nums3 N
   INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;

私はビットカウントのページに行って読んだのですが、％255を実行せずに、ビット演算を使用すると、パフォーマンスが向上する可能性があると思います。機会があれば、それを試して、それがどのように積み重なるかを確認します。

私のパフォーマンスの主張は、ORDERBY句なしで実行されたクエリに基づいています。わかりやすくするために、このコードが実行しているのは、Numに設定されている1ビットの数をカウントすることです。 Numbersから テーブル。これは、セットのどの要素が現在の組み合わせにあるかを選択するための一種のインデクサーとして数値が使用されているため、1ビットの数は同じになります。

気に入っていただければ幸いです！

ちなみに、整数のビットパターンを使用してセットのメンバーを選択するこの手法は、私が「垂直クロス結合」と名付けたものです。これにより、複数のデータセットのクロス結合が効果的に行われ、セットとクロス結合の数は任意になります。ここで、セット数は一度に取られるアイテムの数です。

実際には、通常の水平方向の交差結合（各結合で既存の列リストに列を追加する）は次のようになります。

SELECT
   A.Value,
   B.Value,
   C.Value
FROM
   @Set A
   CROSS JOIN @Set B
   CROSS JOIN @Set C
WHERE
   A.Value = 'A'
   AND B.Value = 'B'
   AND C.Value = 'C'

上記の私のクエリは、1回の結合だけで、必要な回数だけ効果的に「クロス結合」します。確かに、結果は実際のクロス結合と比較してピボットされていませんが、それは小さな問題です。

コードの批評

まず、階乗UDFにこの変更を提案できますか：

ALTER FUNCTION dbo.Factorial (
   @x bigint
)
RETURNS bigint
AS
BEGIN
   IF @x <= 1 RETURN 1
   RETURN @x * dbo.Factorial(@x - 1)
END

これで、はるかに大きな組み合わせのセットを計算できるようになり、さらに効率的になりました。 decimal(38, 0)の使用を検討することもできます 組み合わせ計算でより大きな中間計算を可能にします。

次に、指定されたクエリは正しい結果を返しません。たとえば、以下のパフォーマンステストのテストデータを使用すると、セット1はセット18と同じです。クエリはスライディングストライプを取り巻くように見えます。各セットは常に5つの隣接するメンバーであり、次のようになります（ピボットしました）。見やすくするため）：

 1 ABCDE            
 2 ABCD            Q
 3 ABC            PQ
 4 AB            OPQ
 5 A            NOPQ
 6             MNOPQ
 7            LMNOP 
 8           KLMNO  
 9          JKLMN   
10         IJKLM    
11        HIJKL     
12       GHIJK      
13      FGHIJ       
14     EFGHI        
15    DEFGH         
16   CDEFG          
17  BCDEF           
18 ABCDE            
19 ABCD            Q

クエリのパターンを比較します：

 31 ABCDE  
 47 ABCD F 
 55 ABC EF 
 59 AB DEF 
 61 A CDEF 
 62  BCDEF 
 79 ABCD  G
 87 ABC E G
 91 AB DE G
 93 A CDE G
 94  BCDE G
103 ABC  FG
107 AB D FG
109 A CD FG
110  BCD FG
115 AB  EFG
117 A C EFG
118  BC EFG
121 A  DEFG
...

興味のある人のためにビットパターン->組み合わせ物のインデックスを駆動するために、バイナリの31 =11111であり、パターンがABCDEであることに注意してください。バイナリの121は1111001で、パターンはA__DEFG（後方マッピング）です。

実数テーブルを使用したパフォーマンス結果

上記の2番目のクエリで、大きなセットを使用してパフォーマンステストを実行しました。現時点では、使用したサーバーバージョンの記録がありません。これが私のテストデータです：

DECLARE
   @k int,
   @n int;

DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;

DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);

Peterは、この「垂直クロス結合」は、回避するCROSSJOINを実際に実行するための動的SQLの記述と同様に機能しないことを示しました。数回の読み取りというわずかなコストで、彼のソリューションのメトリックは10倍から17倍優れています。彼のクエリのパフォーマンスは、作業量が増えるにつれて私のものよりも速く低下しますが、だれもそれを使用できないようにするほど速くはありません。

以下の2番目の数値セットは、スケーリング方法を示すために、表の最初の行で割った係数です。

エリック

Items  CPU   Writes  Reads  Duration |  CPU  Writes  Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5    7344     0     3861    8531  |
18•9   17141     0     7748   18536  |   2.3          2.0      2.2
20•10  76657     0    34078   84614  |  10.4          8.8      9.9
21•11 163859     0    73426  176969  |  22.3         19.0     20.7
21•20 142172     0    71198  154441  |  19.4         18.4     18.1

ピーター

Items  CPU   Writes  Reads  Duration |  CPU  Writes  Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5     422    70    10263     794  | 
18•9    6046   980   219180   11148  |  14.3   14.0   21.4    14.0
20•10  24422  4126   901172   46106  |  57.9   58.9   87.8    58.1
21•11  58266  8560  2295116  104210  | 138.1  122.3  223.6   131.3
21•20  51391     5  6291273   55169  | 121.8    0.1  613.0    69.5

外挿すると、最終的には私のクエリの方が安くなりますが（読み取りの最初からですが）、長くはかかりません。セット内の21個のアイテムを使用するには、2097152までの数値テーブルがすでに必要です...

これは、私のソリューションがオンザフライの数値テーブルを使用すると大幅にパフォーマンスが向上することに気付く前に私が最初に行ったコメントです。

オンザフライの数値表を使用したパフォーマンス結果

私が最初にこの答えを書いたとき、私は言いました：

さて、私はそれを試しました、そして結果はそれがはるかに良く機能するということでした！使用したクエリは次のとおりです。

DECLARE @N int = 16, @K int = 12;

CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set 
SELECT TOP (@N) V
FROM
   (VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
   @N int = (SELECT Count(*) FROM #Set),
   @K int = (SELECT TOP 1 Num FROM #Items);

DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
   SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
   FROM Nums
   WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
   SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
   FROM Nums1
), Nums3 AS (
   SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
   FROM Nums2
), BaseSet AS (
   SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
   FROM #Set
)
SELECT
   @Combination = N.Num,
   @Value = S.Value
FROM
   Nums3 N
   INNER JOIN BaseSet S
      ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;

すべてをテストするために必要な時間とメモリを削減するために、値を変数に選択したことに注意してください。サーバーは引き続きすべて同じ作業を行います。 Peterのバージョンを同じように変更し、不要な余分なものを削除して、両方を可能な限り無駄のないものにしました。これらのテストに使用されるサーバーのバージョンは、Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) VM上で実行されています。

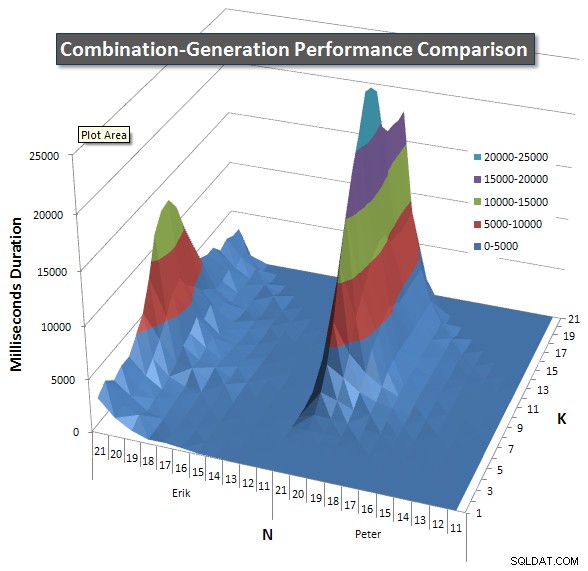
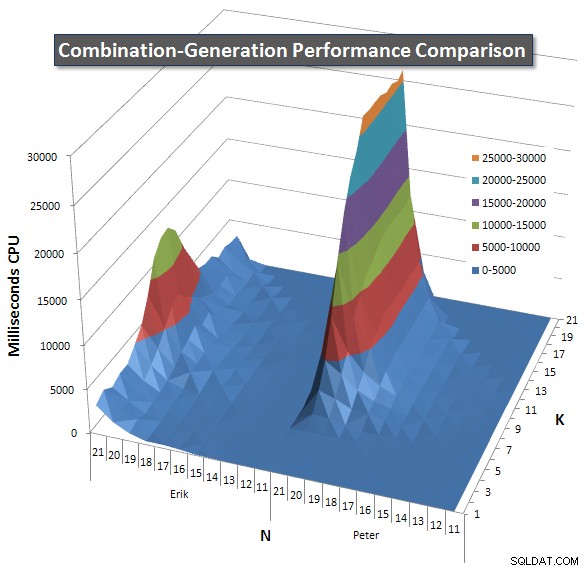
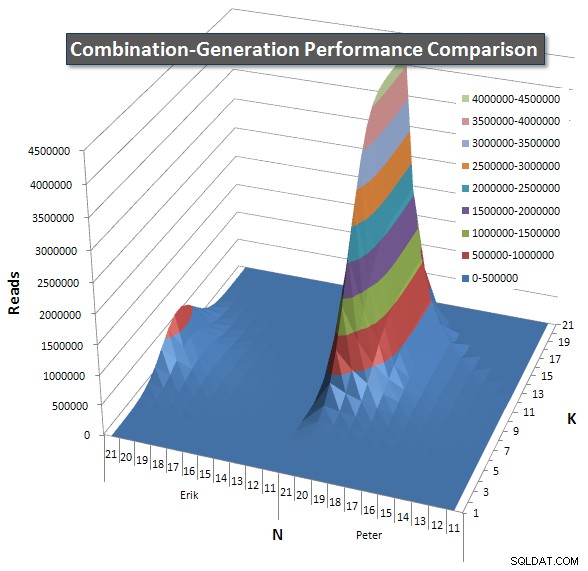
以下は、21までのNとKの値のパフォーマンス曲線を示すグラフです。それらの基本データはこのページの別の回答 。値は、各K値とN値で各クエリを5回実行した後、各メトリックの最良値と最悪値を破棄し、残りの3つを平均した結果です。

基本的に、私のバージョンでは、Nの値が高くKの値が低い「ショルダー」（グラフの左端）があり、動的SQLバージョンよりもパフォーマンスが低下します。ただし、これはかなり低く一定であり、N=21およびK=11付近の中央のピークは、動的SQLバージョンよりも、期間、CPU、および読み取りではるかに低くなっています。

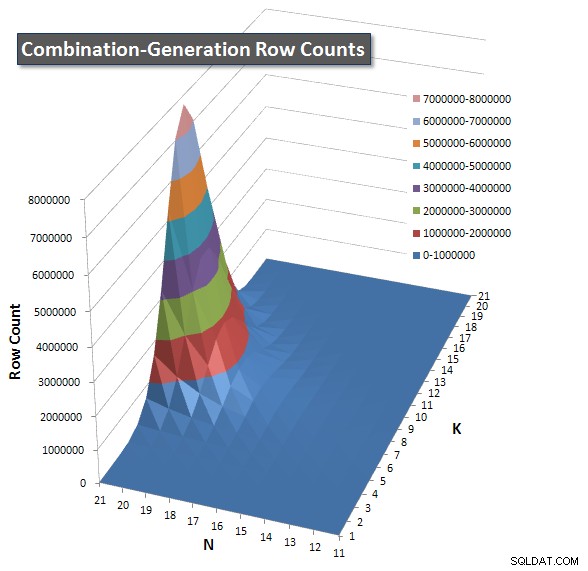
各アイテムが返すと予想される行数のグラフを含めたので、クエリの実行方法と、実行する必要のあるジョブの大きさを比較できます。

このページの追加の回答 をご覧ください。 完全なパフォーマンス結果については。投稿文字数の制限に達し、ここに含めることができませんでした。 （他にどこに置くべきアイデアはありますか？）私の最初のバージョンのパフォーマンス結果に対して物事を展望するために、これは以前と同じフォーマットです：

エリック

Items  CPU  Duration  Reads  Writes |  CPU  Duration  Reads 
----- ----- -------- ------- ------ | ----- -------- -------
17•5    354      378   12382      0 |
18•9   1849     1893   97246      0 |   5.2      5.0     7.9
20•10  7119     7357  369518      0 |  20.1     19.5    29.8
21•11 13531    13807  705438      0 |  38.2     36.5    57.0
21•20  3234     3295     48       0 |   9.1      8.7     0.0

ピーター

Items  CPU  Duration  Reads  Writes |  CPU  Duration  Reads 
----- ----- -------- ------- ------ | ----- -------- -------
17•5     41       45    6433      0 | 
18•9   2051     1522  214021      0 |  50.0     33.8    33.3
20•10  8271     6685  864455      0 | 201.7    148.6   134.4
21•11 18823    15502 2097909      0 | 459.1    344.5   326.1
21•20 25688    17653 4195863      0 | 626.5    392.3   652.2

結論

• オンザフライの数値テーブルは、行を含む実際のテーブルよりも優れています。これは、大量の行数で1つを読み取るには、多くのI/Oが必要になるためです。少しのCPUを使用することをお勧めします。
• 私の最初のテストは、2つのバージョンのパフォーマンス特性を実際に示すのに十分な広さではありませんでした。
• Peterのバージョンは、各JOINを前のアイテムよりも大きくするだけでなく、セットに収める必要のあるアイテムの数に基づいて最大値を制限することで改善できます。たとえば、一度に21個取得された21個のアイテムでは、21行の回答は1つだけです（21個すべてのアイテムを一度に）が、動的SQLバージョンの中間行セットには、実行プランの初期段階で、次のような組み合わせが含まれています。使用可能な「U」より高い値がないため、これは次の結合で破棄されますが、ステップ2の「AU」。同様に、ステップ5の中間行セットには「ARSTU」が含まれますが、この時点で有効なコンボは「ABCDE」のみです。この改善されたバージョンでは、中央に低いピークがないため、明確な勝者になるには十分に改善されていない可能性がありますが、少なくとも対称になり、チャートが領域の中央を超えて最大に留まらず、フォールバックします私のバージョンと同じように0に近くなります（各クエリのピークの上隅を参照してください）。

期間分析

• 一度に12個のアイテムを14個取得するまで、期間（> 100ms）のバージョン間で実際に大きな違いはありません。これまでのところ、私のバージョンは30回勝ち、動的SQLバージョンは43回勝ちます。
• 14•12から、私のバージョンは65倍（59> 100ms）、動的SQLバージョンは64倍（60> 100ms）高速でした。ただし、私のバージョンの方が常に高速だったため、合計で平均256.5秒節約でき、動的SQLバージョンの方が高速だった場合は、80.2秒節約できました。
• すべての試行の平均所要時間の合計は、Erik 270.3秒、Peter446.2秒でした。
• 使用するバージョンを決定するためにルックアップテーブルが作成された場合（入力に対してより高速なバージョンを選択）、すべての結果を188.7秒で実行できます。毎回最も遅いものを使用すると、527.7秒かかります。

読み取り分析

期間分析では、クエリがかなりの量で勝っていることを示しましたが、過度に多くはありませんでした。指標を読み取りに切り替えると、まったく異なる状況が浮かび上がります。私のクエリでは、平均して読み取りの1/10が使用されます。

• 一度に9つのアイテムを取得するまで、読み取り（> 1000）のバージョン間に実際に大きな違いはありません。これまでのところ、私のバージョンは30回勝ち、動的SQLバージョンは17回勝ちます。
• 9•9から、私のバージョンでは118回（113> 1000）、動的SQLバージョンでは69回（31> 1000）の読み取りが少なくなりました。ただし、私のバージョンでは常に読み取り数が少なく、平均で75.9Mの読み取りが節約され、動的SQLバージョンの方が高速であると、38万の読み取りが節約されました。
• すべての試行の平均読み取りの合計は、Erik 8.4M、Peter84Mでした。
• 使用するバージョンを決定するためにルックアップテーブルが作成された場合（入力に最適なバージョンを選択）、すべての結果を800万回の読み取りで実行できます。毎回最悪のものを使用すると、8,430万回の読み取りが必要になります。

上で説明したように、各ステップで選択された項目に追加の上限を設定する、更新された動的SQLバージョンの結果を確認したいと思います。

補遺

次のバージョンのクエリでは、上記のパフォーマンス結果よりも約2.25％向上しています。 MITのHAKMEMビットカウント方法を使用し、Convert(int)を追加しました row_number()の結果について それはbigintを返すので。もちろん、これが上記のすべてのパフォーマンステスト、チャート、およびデータに使用したバージョンであることを望みますが、手間がかかるため、やり直すことはほとんどありません。

WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
   SELECT Convert(int, Num) Num
   FROM Nums
   WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
   SELECT
      Num,
      P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
   FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
   N.Num,
   S.Value
FROM
   Nums3 N
   INNER JOIN BaseSet S
      ON N.Num & S.Ind <> 0
WHERE
   Bits = @K

そして、ビット数を取得するためにルックアップを行うもう1つのバージョンを表示することに抵抗できませんでした。他のバージョンよりも高速な場合もあります：

DECLARE @BitCounts binary(255) = 
   0x01010201020203010202030203030401020203020303040203030403040405
   + 0x0102020302030304020303040304040502030304030404050304040504050506
   + 0x0102020302030304020303040304040502030304030404050304040504050506
   + 0x0203030403040405030404050405050603040405040505060405050605060607
   + 0x0102020302030304020303040304040502030304030404050304040504050506
   + 0x0203030403040405030404050405050603040405040505060405050605060607
   + 0x0203030403040405030404050405050603040405040505060405050605060607
   + 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
   @Combination = N.Num,
   @Value = S.Value
FROM
   Nums1 N
   INNER JOIN BaseSet S
      ON N.Num & S.Ind <> 0
WHERE
   @K =
      Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
      + Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
      + Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
      + Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))