この記事では、COUNT(*)の述語の選択性とカーディナリティの推定について説明します。 HAVINGに見られるような式 条項。詳細は、それ自体が興味深いものになることを願っています。また、カーディナリティ推定器で使用される一般的なアプローチとアルゴリズムのいくつかについての洞察も提供します。
AdventureWorksサンプルデータベースを使用した簡単な例:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
SQLServerがHAVINGのカウント式の述語の推定値をどのように導出するかを確認することに関心があります。 条項。
もちろん、HAVING 節は単なるシンタックスシュガーです。同様に、派生テーブルまたは一般的なテーブル式を使用してクエリを作成することもできます。
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
WHERE G.Expr1001 = 1; 3つのクエリフォームはすべて、同じクエリプランハッシュ値を使用して同じ実行プランを生成します。
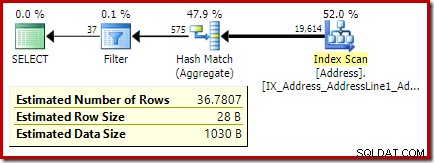
実行後(実際の)計画は、総計の完全な見積もりを示しています。ただし、HAVINGの見積もり 句フィルター(または他のクエリ形式の同等のもの)は不十分です:
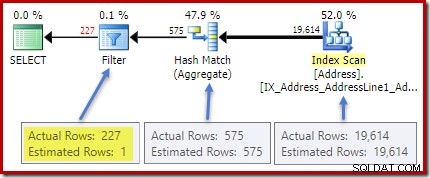
Cityの統計 列には、個別の都市値の数に関する正確な情報が表示されます:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
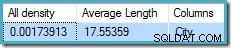
すべての密度 図は、一意の値の数の逆数です。単純に計算すると(1 / 0.00173913)= 575 集計のカーディナリティ推定値を示します。都市ごとにグループ化すると、明らかに、個別の値ごとに1つの行が生成されます。
すべての密度に注意してください 密度ベクトルから来ます。誤って密度を使用しないように注意してください DBCC SHOW_STATISTICSの統計ヘッダー出力からの値 。ヘッダー密度は、下位互換性のためにのみ維持されます。最近のカーディナリティ推定中にオプティマイザによって使用されることはありません。
問題
アグリゲートは、Expr1001というラベルの付いた新しい計算列をワークフローに導入します 実行計画で。 COUNT(*)の値が含まれています グループ化された各出力行:
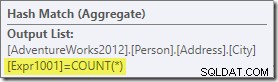
この新しい計算列に関する統計情報はデータベースに明らかにありません。オプティマイザは575行になることを知っていますが、分布については何も知りません。 それらの行内のカウント値の数。
まったく何もありません。オプティマイザは、カウント値が正の整数(1、2、3…)になることを認識しています。それでも、COUNT(*) = 1の選択性を正確に推定するために必要なのは、575行間のこれらの整数カウント値の分布です。 述語。
ある種の分布情報をヒストグラムから導き出すことができると思うかもしれませんが、ヒストグラムは特定のカウント情報のみを提供します(EQ_ROWS )ヒストグラムのステップ値。ヒストグラムのステップの間にあるのは要約だけです:RANGE_ROWS 行にはDISTINCT_RANGE_ROWSがあります 明確な値。選択性の見積もりの品質を気にするほど大きいテーブルの場合、テーブルのほとんどがこれらのステップ内の要約で表されている可能性が非常に高くなります。
たとえば、Cityの最初の2行 列のヒストグラムは次のとおりです。
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

これは、「Abingdon」の行が1つだけで、「Abingdon」の後、「Ballard」の前に29行あり、その29行の範囲に19の異なる値があることを示しています。次のクエリは、その29行のステップ内範囲内の一意の値間の行の実際の分布を示しています。
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

ヒストグラムが言ったように、19の異なる値を持つ29の行があります。それでも、そのクエリのカウント列の述語の選択性を評価する根拠がないことは明らかです。たとえば、HAVING COUNT_BIG(*) = 2 5行(アレクサンドリア、アルタデナ、アトランタ、アウグスブルク、オースティンの場合)を返しますが、ヒストグラムからそれを判断する方法はありません。
知識に基づいた推測
SQL Serverが採用するアプローチは、各グループが最も可能性が高いと想定することです。 行の全体的な平均(平均)数を含めるため。これは、単にカーディナリティを一意の値の数で割ったものです。たとえば、20個の一意の値を持つ1000行の場合、SQL Serverは、(1000/20)=グループあたり50行が最も可能性の高い値であると想定します。
元の例に戻ると、これは、計算されたカウント列に(19614/575)〜= 34.1113付近の値が含まれている可能性が「最も高い」ことを意味します。 。 密度以降 は一意の値の数の逆数であり、カーディナリティ*密度として表すこともできます。 =(19614 * 0.00173913)、非常によく似た結果が得られます。
配布
平均値が最も可能性が高いと言うことは、これまでのところ私たちを連れて行くだけです。また、その可能性を正確に確立する必要があります。そして、平均値から離れるにつれて、可能性がどのように変化するか。この例ですべてのグループに正確に34.113行があると仮定すると、あまり「知識のある」推測にはなりません!
SQL Serverは、正規分布を想定してこれを処理します。これは、すでにおなじみの特徴的なベルの形をしています(リンクされたウィキペディアのエントリからの画像):
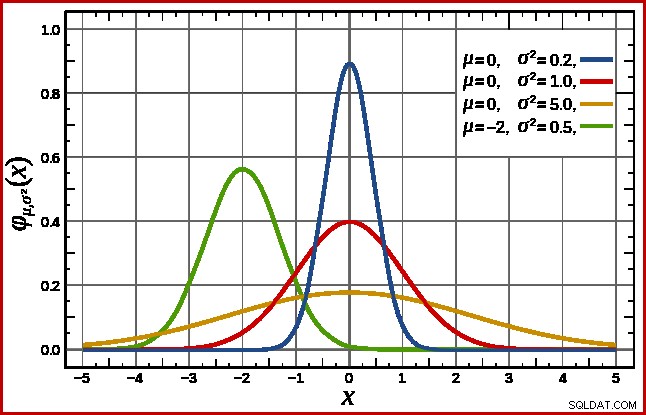
正規分布の正確な形状は、2つのパラメーターによって異なります。 :平均( µ )および標準偏差(σ )。平均は、ピークの位置を決定します。標準偏差は、ベル曲線がどの程度「平坦化」されているかを指定します。曲線が平坦であるほど、ピークは低くなり、確率密度は他の値に分散されます。
SQL Serverは、すでに述べたように、統計情報から平均を導き出すことができます。 標準偏差 計算されたカウント列の値は不明です。 SQL Serverは、これを平方根と推定します。 平均の(後で詳しく説明するわずかな調整あり)。この例では、これは正規分布の2つのパラメーターがおよそ34.1113と5.84(平方根)であることを意味します。
標準 正規分布(上の図の赤い曲線)は、注目に値する特殊なケースです。これは、平均がゼロで、標準偏差が1の場合に発生します。平均を減算して標準偏差で除算することにより、任意の正規分布を標準正規分布に変換できます。
エリアと間隔
選択性の推定に関心があるため、カウント計算列が特定の値(x)を持つ確率を探しています。この確率は、上記のy軸の値ではなく、曲線の下の領域によって与えられます。 xの左側。
平均が34.1113、標準偏差が5.84の正規分布の場合、x=30の左側の曲線の下の領域は約0.2406です。
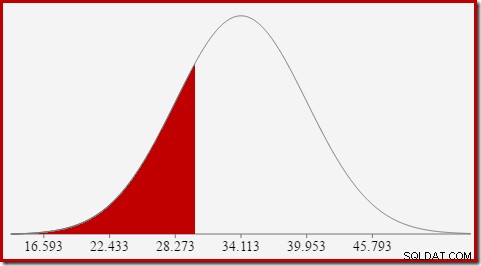
これは、計算されたカウント列が以下である確率に対応します。 クエリ例では30。
これは、一般に、特定の値の確率ではなく、間隔を探しているという考えにうまくつながります。 。おそらくカウントが等しいであることを見つけるため 整数値の場合、整数がサイズ1の区間にまたがるという事実を考慮する必要があります。整数を区間に変換する方法は、いくぶん恣意的です。 SQL Serverは、 0.5を加算および減算することでこれを処理します 間隔の下限と上限を指定します。
たとえば、計算されたカウント値が30に等しい確率を見つけるには、減算する必要があります。 (x =30.5)の面積から(x =29.5)の正規分布曲線の下の面積。結果は、次の図の(29.5
赤いスライスの面積は約0.0533 。最初の適切な概算として、これは、テストクエリでのカウント=30述語の選択性です。
与えられた値の左側の正規分布の下の面積を計算するのは簡単ではありません。一般式は累積分布関数(CDF)で与えられます。問題は、CDFを基本的な数学関数で表現できないため、代わりに数値近似法を使用する必要があることです。
すべての正規分布は標準正規分布(平均=0、標準偏差=1)に簡単に変換できるため、近似はすべて標準正規分布を推定するために機能します。これは、変換する必要があることを意味します クエリに適した特定の正規分布から標準正規分布までの区間境界。これは、前述のように、平均を減算し、標準偏差で除算することによって行われます。
Excelに精通している場合は、特定の正規分布または標準正規分布のCDFを(数値近似法を使用して)計算できる関数NORM.DISTおよびNORM.S.DISTを知っているかもしれません。
SQL Serverに組み込まれているCDF計算機はありませんが、簡単に作成できます。標準正規分布のCDFは次のとおりです。
…ここでerf エラー関数です:
標準正規分布のCDFを取得するためのT-SQL実装を以下に示します。 誤差関数の数値近似を使用します これは、SQL Serverが内部で使用するものに非常に近いものです:
例:テストクエリの正規分布を使用してx =30のCDFを計算するには:
標準正規分布に変換するための正規化手順に注意してください。このプロシージャは値0.2407196…を返します。これは、対応するExcelの結果を小数点以下7桁に一致させます。
次のコードは、サンプルクエリを変更して、フィルターのより大きな推定値を生成します(比較は、以前よりも平均にはるかに近い値32になりました):
オプティマイザーからの見積もりは36.7807になりました 。
見積もりを手動で計算するには、最初にいくつかの最終的な詳細に対処する必要があります。
次の手順には、この記事のすべての詳細が組み込まれています。前述のCDF手順が必要です:
これで、この手順を使用して、新しいテストクエリの見積もりを生成できます。
出力は次のとおりです。
これは、オプティマイザのカーディナリティ推定値である36.7807と非常によく比較されます。
この手順は、同等性テスト以外のカウント間隔にも使用できます。必要なのは
これをプロシージャで使用するには、
結果は572.5964です:
オプティマイザーの見積もりは
繰り返しますが、これはオプティマイザーの見積もりと一致します。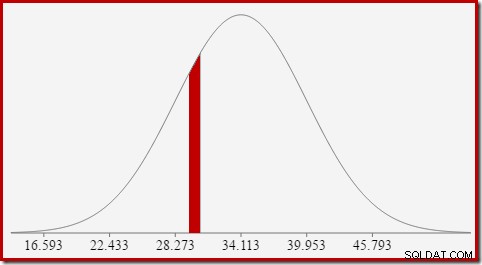
累積分布関数
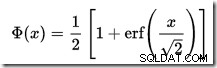
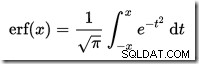
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; 最終的な詳細と例
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1の複雑なロジックがあります。 、ここでは詳しく説明しません。 COUNT(*) = 1以外 この場合、レガシーCEは新しいCE(SQL Server 2014以降で使用可能)と同じロジックを使用します。CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
不等式区間の例
@Fromを設定することだけです および@To 整数区間境界へのパラメータ。無制限を指定するには、ゼロまたはNULLを渡します 好きなように。SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULLを設定します。 および@To = 49 (50は未満によって除外されるため):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEENを使用した最後の例 :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN以降 包括的である場合、プロシージャ@From = 25を渡します。 および@To = 30 。結果は次のとおりです。
